2020/03/31
日米和親条約
3月31日
火曜日
日米和親条約
1854年3月31日
(嘉永7年3月3日)
ペリー提督と江戸幕府の間に
日米和親条約(神奈川条約)が結ばれ、
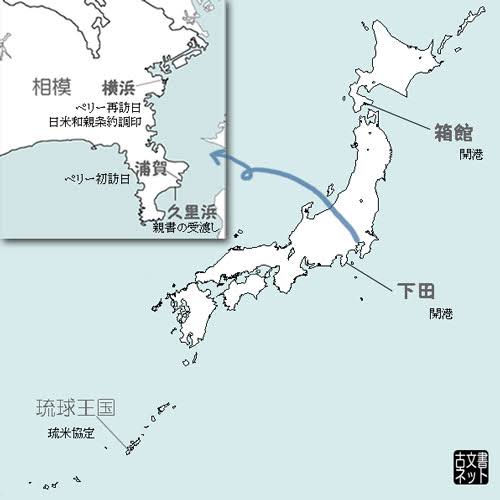
下田・函館が通商港とされる。
日米和親条約(にちべいわしんじょうやく)は、
江戸幕府とアメリカ合衆国が締結した条約である。
神奈川条約とも呼ぶ。
日本側全権は林復斎(大学頭)、
アメリカ側全権は東インド艦隊司令長官の
マシュー・ペリーである。
この条約によって
日本は下田と箱館(現在の函館)を開港し、
鎖国体制は終焉を迎えた。
条約名のうち「日米」とは、
日は日本、米はメリケン(米利堅)で、
当時の日本における正式名は
日本國米利堅合衆國和親條約
(にほんこくめりけんがっしゅうこくわしんじょうやく)である。
幕末から明治にかけては、
アメリカ合衆国は「メリケン」
「米利堅」と呼ばれることが多かった。
英文における正式名称は
「Convention of Peace and Amity between the United States of America and the Empire of Japan
(アメリカ合衆国と日本帝国間の平和および
修好の条約)」であり、
前述のように「Treaty of Kanagawa」と通称される。
2020/03/30
正十七角形
3月30日
月曜日
正十七角形
1796年3月30日
正十七角形が
定規とコンパスだけで作図可能なことを
カール・フリードリヒ・ガウスが発見。
十七角形(じゅうしちかくけい、
じゅうななかっけい、heptadecagon)は、
多角形の一つで、
47本の辺と17個の頂点を持つ図形である。
内角の和は2700°、対角線の本数は119本である。
正十七角形は
定規とコンパスによる作図が可能な図形の一つである。
p が素数である正p角形のうち、
このような作図が可能なものは
p がフェルマー素数である場合に限られる。
具体的には
p = 3, 5, 17, 257, 65537のときで
正三角形、正五角形、正十七角形、正二百五十七角形、
正六万五千五百三十七角形の5つしか知られていない。
正十七角形が
コンパスと定規で作図できることは
1796年3月30日の朝に
19歳のカール・フリードリヒ・ガウスが
目覚めてベッドから起き上がる時に発見した。
これは任意の三角関数において、
その変数としての角が 2π/17 radのとき、
関数の値が有理数と平方根の組み合わせのみで
表現できることを意味する。
さっぱり分からん😅
